第十四章 三角形 单元测试
1、选择题
1、有四条线段，它们的长分别为1CM，2CM，3CM，4CM，从中选三条构成三角形，其中正确的选法有〔〕
A、1种
B、2种
C、3种
D、4种
2、能把一个三角形分成两个面积相等的三角形的是〔〕
A、三角形的中线
B、三角形的高线
C、三角形的角平分线
D、以上都不对
3、假如一个三角形的三条高的交点恰是三角形的一个顶点，那样这个三角形是〔〕
A、锐角三角形
B、钝角三角形
C、直角三角形
D、不可以确定
4、在以下各图形中，分别画出了△ABC中BC边上的高AD，其中正确的选项是〔〕
A、
B、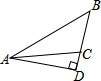
C、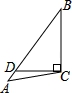
D、
5、如图，工人师傅砌门时，常用木条EF固定矩形门
框ABCD，使其不变形，这种做法的依据是〔〕
A、两点之间线段最短
B、矩形的对称性
C、矩形的四个角都是直角
D、三角形的稳定性
6、△ABC中，∠A＝80°，∠B、∠C的平分线的夹角是〔〕
A、130°
B、60°
C、130°或50°
D、60°或120°
7、一个多边形的各内角都是144度，那样它是〔〕边形、
A、10
B、9
C、8
D、7
8、如图，某同学把一块三角形的玻璃打碎成了三块，目前要到玻璃店去配一块完全一样的玻璃，那样最省事的方法是〔〕
A、带①去
B、带②去
C、带③去
D、带①和②去
9、：如图，AC＝CD，∠B＝∠E＝90°，AC⊥CD，那样不正确的结论是〔〕
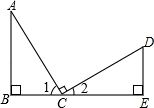
A、∠A与∠D互为余角
B、∠A＝∠2
C、△ABC≌△CED
D、∠1＝∠2
10、如图，将两根钢条AA′、BB′的中点O连在一块，使AA′、BB′能绕着点O自由转动，就做成了一个测量工具，由三角形全等可知A′B′的长等于内槽宽AB，那样断定△OAB≌△OA′B′的原因是〔〕
A、SAS
B、ASA
C、SSS
D、AAS
2、填空题
11、三角形三边分别为1，X，5，那样整数X＝___.
12、如图，RT△ABC中，∠ACB＝90°，∠A＝50°，将它折叠，使点A落在边CB上A′处，折痕为CD，那样∠A′DB为____.
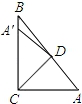
13、在△ABC中，∠A：∠B：∠C＝1：2：3，那样∠A＝_____，∠B＝_____，∠C＝_____.
14、如图，△ABC≌△ADE，∠B＝100°，∠BAC＝30°，那样∠AED＝____.
15、如图，∠1＝∠2，要使△ABE≌△ACE，还需添加一个条件是_________〔填上你觉得适合的一个条件即可〕.
16、：如图，AD是△ABC的角平分线，且AB：AC＝3：2，那样△ABD与△ACD的面积之比为________________.
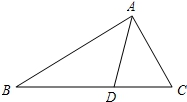
17、如图，在△ABC中，∠A＝50°，∠ABC＝70°，BD平分∠ABC，那样∠BDC的度数是_______________.
18、如图，∠1＋∠2＋∠3＋∠4＋∠5＋∠6＝____.
3、解答卷
19、计算：
〔1〕一个等腰三角形的一边长为8CM，周长为20CM，求其它两边的。
〔2〕等腰三角形的一边长等于6CM，一边长等于7CM，求它的周长。
〔3〕等腰三角形的一边长等于5CM，一边长等于12CM，求它的周长。
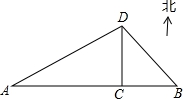
20、如图，有A、B、C、D四个小岛，A、B、C在同一条直线上，而且B、C在A的正东方，D岛在C岛的正北方，A岛在D岛的南偏西52°方向，B岛在D岛的南偏东40°方向、那样∠DAC和∠DBC分别是多少？
21、如图，在三角形ABC中，∠B＝∠C，D是BC上一点，且FD⊥BC，DE⊥AB，∠AFD＝140°，你能求出∠EDF的度数吗？
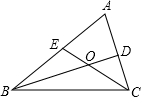
22、如图，武汉有三个车站A、B、C成三角形，一辆公共汽车从B站前往到C站、
〔1〕当汽车运动到点D点时，刚好BD＝CD，连接线段AD，AD这条线段是什么线段？如此的线段在△ABC中有几条呢？此时有面积相等的三角形吗？
〔2〕汽车继续向前运动，当运动到点E时，发现∠BAE＝∠CAE，那样AE这条线段是什么线段呢？在△ABC中，如此的线段又有几条呢？
〔3〕汽车继续向前运动，当运动到点F时，发现∠AFB＝∠AFC＝90°，那样AF是什么线段？如此的线段在△ABC中有几条？
23、如图，要测量河两岸相对的两点A，B的距离，可以在AB的垂线BF上取两点C，D，使CD＝BC，再定出BF的垂线DE，使A，C，E在一条直线上，这个时候测得的DE的长就是AB的长，为何？
参考答案
1、选择题
1、A
剖析：两条较小的边的和大于最大的边即可
解：能构成三角形的只有2、3、4这一种状况、应选A、
点评：考查三角形的边时，应该注意三角形形成的条件：任意两边之和大于第三边，任意两边之差小于第三边、
2、A
考试知识点：三角形的面积；三角形的角平分线、中线和高、
剖析：察看各选项可知，只有三角形的中线把三角形分成等底同高的两个三角形，再依据三角形的面积公式，这两个三角形的面积相等、
解：∵三角形的中线把三角形分成的两个三角形，底边相等，高是同一条高，
∴分成的两三角形的面积相等、
点评：此题考查了等底等高的两个三角形的面积相等的性质，依据此性质，可以解决不少借助三角形的面积进行计算的题目，需熟练学会并灵活运用、
3、C
考试知识点：三角形的角平分线、中线和高、
剖析：依据三角形的高的特征对选项进行一一剖析，即可得出答案、
解：A、锐角三角形，三条高线交点在三角形内，故错误；
B、钝角三角形，三条高线不会交于一个顶点，故错误；
C、直角三角形的直角所在的顶点正好是三条高线的交点，可以得出这个三角形是直角三角形，故正确；
D、能确定C正确，故错误、
点评：此题主要考查了三角形的高，用到的要点是钝角三角形的三条高所在的直线的交点在三角形的外部；锐角三角形的三条高所在的直线的交点在三角形的内部；直角三角形的三条高所在的直线的交点是三角形的直角顶点、
4、B
考试知识点：三角形的角平分线、中线和高、
剖析：三角形的高即从三角形的顶点向对边引垂线，顶点和垂足间的线段、依据定义可知
解答： 解：过点A作直线BC的垂线段，即画BC边上的高AD，所以画法正确的选项是B
点评：此题考查了三角形的高的定义，可以正确作三角形一边上的高、
5、D
剖析：用木条EF固定矩形门框ABCD，即是组成△AEF，故可用三角形的稳定性讲解、
解：加上EF后，原不稳定的四边形ABCD中具备了稳定的△EAF，故这种做法依据的是三角形的稳定性、
点评：此题考查三角形稳定性的实质应用、三角形的稳定性在实质日常有着广泛的应用，如钢架桥、房子架梁等，因此要使一些图形具备稳定的结构，总是通过连接辅助线转化为三角形而获得、
6、C
考试知识点：三角形的角平分线、中线和高；三角形内角和定理、
剖析：作出图形，设两角平分线相交于点O，依据三角形的内角和定理求出∠ABC＋∠ACB的度数，再依据角平分线的概念求出∠OBC＋∠OCB的度数，然后在△BOC中借助三角形的内角和定理求解即可得到∠BOC的度数，再分夹角为钝角与锐角两种状况解答
解：如图，∵∠A＝80°
∴∠ABC＋∠ACB＝180°﹣∠A＝180°﹣80°＝100°
∵BD、CE分别为∠ABC、∠ACB的平分线
∴∠OBC＝
∠ABC，∠OCB＝∠ACB
∴∠OBC＋∠OCB＝〔∠ABC＋∠ACB〕＝×100°＝50°
在△BOC中，∠BOC＝180°﹣〔∠OBC＋∠OCB〕＝180°﹣50°＝130°
又∵180°﹣130°＝50°
∴角平分线的夹角是130°或50°
点评：此题考查了三角形的角平分线的概念，三角形的内角和定理，整体思想的借助比较重点，应该注意夹角有钝角与锐角两种状况、
7、A
考试知识点：多边形内角与外角、
剖析：依据多边形内角和公式〔N﹣2〕•180°计算即可、
解：设它是N边形，由题意得，
〔N﹣2〕×180°＝144N，
解得N＝10
点评：此题考查的是多边形内角的计算，学会多边形内角和是〔N﹣2〕•180°是解题的重点、
8、C
考试知识点：全等三角形的应用、
专题：应用题、
剖析：此题可以使用全等三角形的断定办法与排除法进行剖析，从而确定最后的答案、
解：A、带①去，仅保留了原三角形的一个角和部分边，不可以得到与原来一样的三角形，故A选项错误；
B、带②去，仅保留了原三角形的一部分边，也是不可以得到与原来一样的三角形，故B选项错误；
C、带③去，不但保留了原三角形的两个角还保留了其中一个边，符合ASA断定，故C选项正确；
D、带①和②去，仅保留了原三角形的一个角和部分边，同样不可以得到与原来一样的三角形，故D选项错误、
点评：主要考查学生对全等三角形的断定办法的灵活运用，需要对常见的几种办法熟练学会、
9、D
考试知识点：全等三角形的断定与性质、
剖析：先依据角角边证明△ABC与△CED全等，再依据全等三角形对应边相等，全等三角形的对应角相等的性质对各选项判断后，借助排除法求解、
解：∵AC⊥CD，
∴∠1＋∠2＝90°
∵∠B＝90°
∴∠1＋∠A＝90°
∴∠A＝∠2
在△ABC和△CED中，
∴△ABC≌△CED〔AAS〕
故B、C选项正确；
∵∠2＋∠D＝90°
∴∠A＋∠D＝90°
故A选项正确；
∵AC⊥CD，
∴∠ACD＝90°
∠1＋∠2＝90°
故D选项错误
点评：此题主要考查全等三角形的性质，先证明三角形全等是解决此题的突破口，也是难题所在、做题时，要结合条件与全等的断定办法对选项逐一验证、
10、A
考试知识点：全等三角形的应用
剖析：由O是AA′、BB′的中点，可得AO＝A′O，BO＝B′O，再有∠AOA′＝∠BOB′，可以参考全等三角形的断定办法SAS，断定△OAB≌△OA′B′
解：∵O是AA′、BB′的中点，
∴AO＝A′O，BO＝B′O
在△OAB和△OA′B′中
∴△OAB≌△OA′B′〔SAS〕
点评：此题主要全等三角形的应用，重点是学会全等三角形的断定办法：SSS、SAS、ASA、AAS，HL，要证明两个三角形全等，需要有对应边相等这一条件、
2、填空题
11、考试知识点：三角形三边关系、
剖析：依据三角形的三边关系定理三角形两边之和大于第三边；三角形的两边差小于第三边可确定X的取值范围，再找出符合条件的整数即可、
解：依据三角形的三边关系定理可得：5﹣1《X《5＋1，
解得：4《X《6，
∵X为整数
∴X＝5，
故答案为：5
点评：此题主要考查了三角形的三边关系，重点是学会第三边的范围是：大于的两边的差，而小于两边的和、
12、考试知识点：轴对称的性质；三角形的外角性质
剖析：依据轴对称的性质可知∠CA′D＝∠A＝50°，然后依据外角定理可得出∠A′DB
解：由题意得：∠CA′D＝∠A＝50°，∠B＝40°
由外角定理可得：∠CA′D＝∠B＋∠A′DB
∴可得：∠A′DB＝10°
故答案为：10°
点评：此题考查轴对称的性质，是基础题，注意料之外角定理的运用是解决此题的重点、
13、考试知识点：三角形内角和定理、
剖析：设∠A＝X°，∠B＝2X°，∠C＝3X°，依据∠A＋∠B＋∠C＝180°得出方程X＋2X＋3X＝180，求出X即可
解：∵∠A：∠B：∠C＝1：2：3
∴设∠A＝X°，∠B＝2X°，∠C＝3X°
∵∠A＋∠B＋∠C＝180°
∴X＋2X＋3X＝180
X＝30，
∴∠A＝30°，∠B＝60°，∠C＝90°
故答案为：30°，60°，90°
点评：此题考查了三角形内角和定理的应用，注意：三角形的内角和等于180°，用了方程思想
14、考试知识点：全等三角形的性质、
剖析：先运用三角形内角和定理求出∠C，再运用全等三角形的对应角相等来求∠AED
解：∵在△ABC中，∠C＝180﹣∠B﹣∠BAC＝50°
又∵△ABC≌△ADE
∴∠AED＝∠C＝50°
∴∠AED＝50度
故填50
点评：此题考查的是全等三角形的性质，全等三角形的对应边相等，对应角相等、是需要识记的内容、
15、考试知识点：全等三角形的断定、
剖析：依据题意，易得∠AEB＝∠AEC，又AE公共，所以依据全等三角形的断定办法容易探寻添加条件、
解：∵∠1＝∠2，∴∠AEB＝∠AEC
又AE公共
∴当∠B＝∠C时，△ABE≌△ACE〔AAS〕
或BE＝CE时，△ABE≌△ACE〔SAS〕
或∠BAE＝∠CAE时，△ABE≌△ACE〔ASA〕
点评：此题考查三角形全等的断定办法，断定两个三角形全等的一般办法有：SSS、SAS、ASA、AAS、HL、
注意：AAA、SSA不可以断定两个三角形全等，断定两个三角形全等时，需要有边的参与，假设有两边一角对应相等时，角需要是两边的夹角、
16、考试知识点：角平分线的性质、
剖析：此题需先借助角平分线的性质可知点D到AB、AC的距离相等，即两三角形的高相等，察看△ABD与△ACD，面积比即为AB、AC的比，答案可得、
解：∵AD是△ABC的角平分线，
∴点D到AB的距离等于点D到AC的距离，
又∵AB：AC＝3：2，
那样△ABD与△ACD的面积之比为3：2
故答案为：3：2
点评：此题考查了角平分线的性质；此题的重点是依据角平分线的性质，求得点D到AB的距离等于点D到AC的距离，即△ABD边AB上的高与△ACD边AC上的高相等、
17、考试知识点：三角形内角和定理、
剖析：依据三角形内角和得出∠C＝60°，再借助角平分线得出∠DBC＝35°，进而借助三角形内角和得出∠BDC的度数、
解：∵在△ABC中，∠A＝50°，∠ABC＝70°
∴∠C＝60°
∵BD平分∠ABC
∴∠DBC＝35°
∴∠BDC＝180°﹣60°﹣35°＝85°、
故答案为：85°
点评：此题考查了角平分线的概念，三角形内角和定理等常识，解答此题的重点是依据三角形内角和得出∠C＝60°，再借助角平分线得出∠DBC＝35°、
18、考试知识点：三角形的外角性质
剖析：依据三角形外角的性质知∠1＋∠2＝∠BOD，∠3＋∠4＝∠FOD，∠5＋∠6＝BOF，那样易求∠1＋∠2＋∠3＋∠4＋∠5＋∠6的值、
解：如图，∵∠1＋∠2＝∠BOD，∠3＋∠4＝∠FOD，∠5＋∠6＝BOF，
∴∠1＋∠2＋∠3＋∠4＋∠5＋∠6＝∠BOD＋∠FOD＋∠BOF＝360°
故答案是：360°
点评：此题考查了三角形的外角性质、解答的重点是交流外角和内角的关系、
3、解答卷
19、考试知识点：等腰三角形的性质；三角形三边关系、
剖析：〔1〕条件中，此题没明确说明的边长是不是是腰长，所以有两种状况讨论，还应断定能否组成三角形；
〔2〕分6是等腰三角形的腰长与底边两种状况讨论求解；
〔3〕题目给出等腰三角形有两条边长为5CM和12CM，而没明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形、
解：〔1〕①底边长为8，那样腰长为：÷2＝6，所以另两边的长为6CM，6CM，能构成三角形；
②腰长为8，那样底边长为：20﹣8×2＝4，底边长为8CM，另一个腰长为4CM，能构成三角形、
因此另两边长为8CM、4CM或6CM、6CM；
〔2〕①6是腰长时，周长＝6＋6＋7＝19；
②6是底边时，7是腰，周长＝6＋7＋7＝20；
综上，它的周长为19或20；
〔3〕分两种状况：
当腰为5CM时，5＋5《12，所以不可以构成三角形；
当腰为12CM时，12＋12》5，12﹣12《5，所以能构成三角形，周长是：12＋12＋5＝29CM
点评：考查了等腰三角形的性质和三角形的三边关系；没明确腰和底边的题目必须要想到两种状况，分类进行讨论，还应验证各种状况是不是能构成三角形进行解答，这点尤为重要，也是解题的重点、
20、考试知识点：方向角
剖析：由D岛在C岛的正北方，可知DC⊥AB，借助三角形的内角和求得答案即可、
解：∵D岛在C岛的正北方，A岛在D岛的南偏西52°方向，B岛在D岛的南偏东40°方向，
∴∠ADC＝52°，∠BCD＝40°
∴∠DAC＝90°﹣∠ADC＝38°，∠DBC＝90°﹣∠BCD＝50°
点评：此题考查方向角的概念，三角形的内角和定理，理清方位角的意义是解决问题的重点、
21、考试知识点：等腰三角形的性质
剖析：因为DF⊥BC，DE⊥AB，所以∠FDC＝∠FDB＝∠DEB＝90°，又由于△ABC中，∠B＝∠C，所以∠EDB＝∠DFC，由于∠AFD＝140°，所以∠EDB＝∠DFC＝40°，所以∠EDF＝90°﹣∠EDB＝50°、
解：∵DF⊥BC，DE⊥AB，
∴∠FDC＝∠FDB＝∠DEB＝90°
又∵∠B＝∠C
∴∠EDB＝∠DFC
∵∠AFD＝140°
∴∠EDB＝∠DFC＝40°
∴∠EDF＝90°﹣∠EDB＝50°
点评：此题考查了等腰三角形的性质；借助三角形的内角和定理求解角的度数是正确解答此题的重点
22、考试知识点：三角形的角平分线、中线和高
剖析：〔1〕因为BD＝CD，那样点D是BC的中点，AD是中线，三角形的中线把三角形分成两个面积相等的三角形；
〔2〕因为∠BAE＝∠CAE，由AE是三角形的角平分线；
〔3〕因为∠AFB＝∠AFC＝90°，那样AF是三角形的高线
解：〔1〕AD是△ABC中BC边上的中线，三角形中有三条中线、此时△ABD与△ADC的面积相等、
〔2〕AE是△ABC中∠BAC的角平分线，三角形上角平分线有三条、
〔3〕AF是△ABC中BC边上的高线，高线有时在三角形外部，三角形中有三条高线、
点评：此题考查了三角形的高线、角平分线、中线的定义，它们分别都有三条、
23、考试知识点：全等三角形的应用
剖析：此题是测量两点之间的距离办法中的一种，符合全等三角形全等的条件，策略的操作性强，只须测量的线段和角度在陆地一侧即可推行、
解：∵AB⊥BF，DE⊥BF
∴∠ABC＝∠EDC＝90°
又∵直线BF与AE交于点C
∴∠ACB＝∠ECD〔对顶角相等〕
∵CD＝BC
∴△ABC≌△EDC
∴AB＝ED
即测得DE的长就是A，B两点间的距离
点评：此题考查了全等三角形的应用；解答此题的重点是设计三角形全等，巧妙地借用两个三角形全等，做题时应该注意探寻所求线段与线段之间的等量关系。
